We here a lot about FM for synthesis - but the truth is that most 'FM' is not Frequency Modulation at all - it is Phase Modulation.
...The full example patch is at the bottom of this post...
The reason is simply that Phase Modulation can produce much the same effects as Frequency Modulation but it is much easier to get correct. Let us look into why this by first having a quick look at what Frequency and Phase modulation actually are. I am going to start at the well read amateur level here.
The reason is simply that Phase Modulation can produce much the same effects as Frequency Modulation but it is much easier to get correct. Let us look into why this by first having a quick look at what Frequency and Phase modulation actually are. I am going to start at the well read amateur level here.
- As we know - a note has a pitch.
- Another word for pitch is (ish) frequency. Frequency is more precise in its usage than pitch so we shall use it instead.
- So, A4 is 440Hz which is a frequency.
- A pure note is a sine wave. This means the pressure waves in air for that note follow a sinusoidal shape. Equally, the voltage in an amplifier or synthesiser circuit will follow a sinusoidal shape (again - ish).
- A pure note has just one frequency in it.
- However, we want to create non pure tones (as pure ones are boring in general). If you don't believe me that a pure note is boring and that something like a flute makes a pure note - think again http://www.soundonsound.com/sos/oct03/articles/synthsecrets.htm. Even a flute has a very complex tone.
- We can make rich tones in many ways, but Frequency Modulation of a pure tone is one of the more interesting.
Frequency Modulation Step By Step So we have a pure tone and we slowly move its frequency down a bit and then up a bit and back to the middle. What we get is vibrato (tremolo being the amplitude equivalent). Vibrato is technically frequency modulation but not in the sense that syntheses nerds talk about FM. The interesting stuff happens when we modulate the frequency of a tone up and down as a rate similar to that frequency of the tone its self. In other words, the tone (carrier) and modulation are both in the audible range.
Frequency modulating (let's drop the caps for now) a tone of 1000Hz with a tone of 1100Hz will produce a tone with tones inside it rather than vibrato. In this case we will get 1000, 2100, 4200 and so on. There are also things which are called (sorry - I know it sounds confusing) negative frequencies. Now, negative frequencies cannot actually exist in sound though they are important in the mathematical modelling of sound. In real sound they are just frequencies.
A bit confused? Here is a simple way of looking at it:
- We take a fundamental of frequency X.
- We frequency modulate it with frequency Y.
- We get new frequencies along side X, these are X+Y, X+Yx2, X+Yx3 etc.
- We also get X-Y, X-Yx2, X-Yx3 etc.
- However, the ones where we take some multiple Y away from X might end up negative.
- So, X=1000 and Y=1100 then X-Y=-100Hz.
- Negative frequencies don't exist in sound so we actually get the positive equivalent - e,.g. 100Hz.
This means that 1000Hz frequency modulated with 1100Hz will give:
- 100,
- 1000,
- 1200,
- 2100,
- 2300,
- 3200
- ...
Consequently, what we are left with is the original (fundamental) and a mixture of inharmonic overtones (and under-tones which we often remove via filtering). We will also notice that the contribution of each inharmonic overtone reduces as the frequency goes up.
What does all this sound like?
Well, the 1000m1100 example will sound quite bell like. But, the truth is that, frequency modulation will make pretty much any tone you want (especially with a bit of filtering). This is why it is so powerful. Other techniques like wave shaping and distortion will produce just the harmonic overtones of the fundamental. Amplitude modulation will produce inharmonic over and under-tones but only one. Ring modulation is similarly more limited than FM. Nothing (other than additive synthesis which can do anything in theory) is quite as powerful at creating rich sounds.
But - why still using it when we have additive synthesis? I mentioned additive synthesis. As I say, this can produce any sound; so why bother with anything but additive synthesis. Why go to the effort of creating FM? The reasons are two fold. Firstly, to create a really complex rich sound with additive synthesis is very computationally complex and therefore still (even with modern technology) poses a major challenge to synthesis engines. Just creating a single waveform with additive synthesis is not so bad, but a complex evolving tone is quite a challenge. The second reason is very human: creativity is iterative. We make a sound we like it, we tweak it, we listen, we get inspired, we change it and we keep going. Frequency modulation gives an jaw dropping capacity to shape the resulting sound with only a few parameters to tweak, this makes it ideal for creative exploration.
From Bells To Clarinets
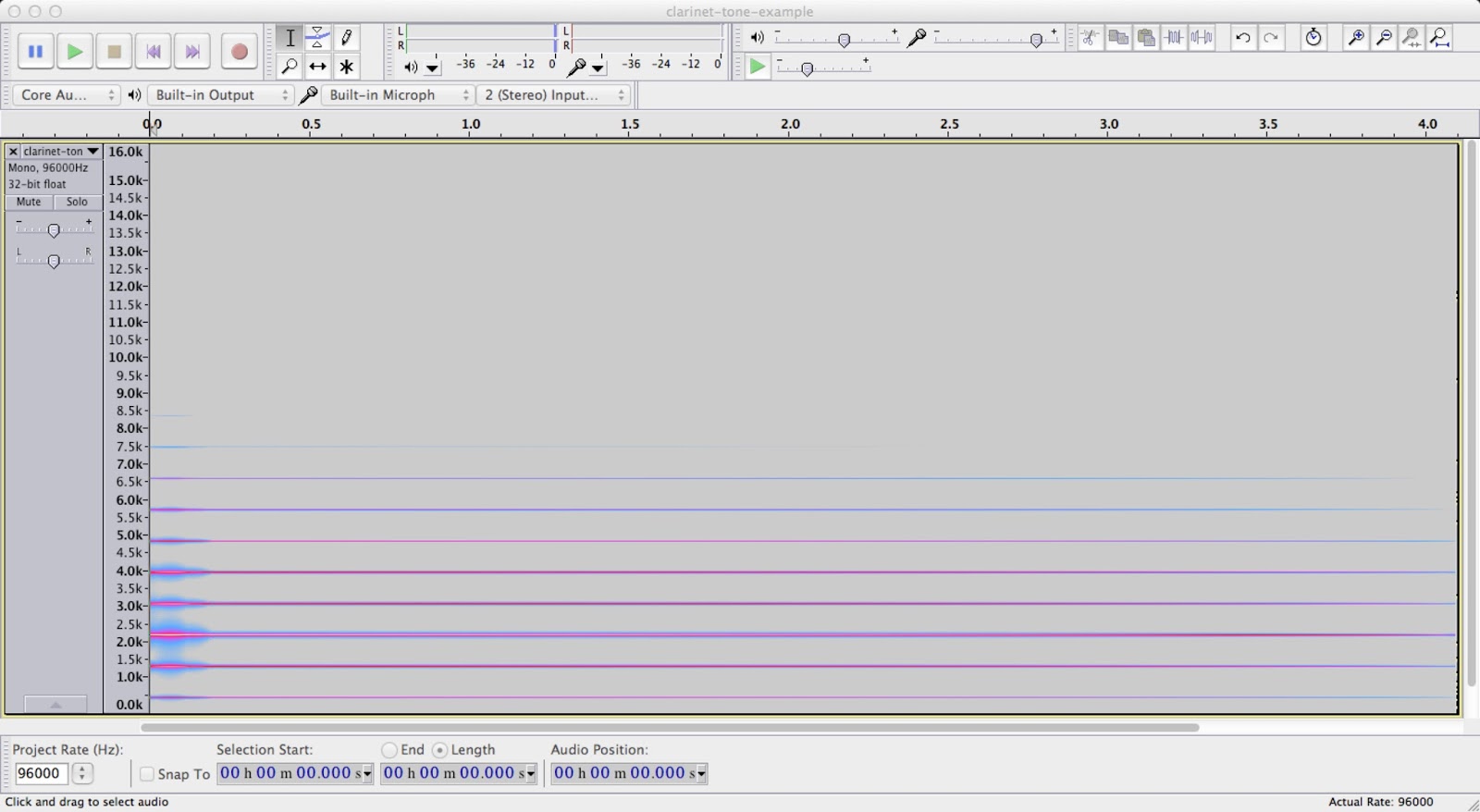
By controlling difference in frequency of the modulation and fundamental and the amount of modulation (sometimes called the modulation index) we get all sorts of different tones. Here are some example spectrograms. I have not filtered these so two have the low under-tones in them:
 |
| Modulation of 440Hz with 440.88Hz producing a spread harmonic spectrum similar to a low pitched piano note of a guitar string. |
 |
| A classic bell tone modulating 440Hz with 528Hz. |
The above notes all had an ADSR envelope applied which gives the characteristic intensity shape seen left to right.
From Frequency To Phase
My examples above are a cheat because they were not produced with frequency modulation; I used phase modulation. Here is the Sonic Field patch which created these tones:
{
(
(0,0),
(?a,1),
(?d,0.5),
(?s,0.1)
(?r,0.0)
)NumericShape !env
(
?frequency,
(
((1,(?r,(?frequency,?frequency-spacing)*)ExactSinWave)DirectMix,?modulation-amount)NumericVolume
)Mix
)PhaseModulatedSinWave !signal
(
>signal,
>env
) Multiply Normalise,
}!play-bell-inner
64 !a
128 !d
2024 !s
4096 !r
440 !frequency
0.15 !modulation-amount
1.2 !frequency-spacing
((?play-bell-inner Do),"temp/bell-tone-example.wav")WriteFile32
0.35 !modulation-amount
1.002 !frequency-spacing
((?play-bell-inner Do),"temp/string-tone-example.wav")WriteFile32
0.5 !modulation-amount
2.0 !frequency-spacing
((?play-bell-inner Do),"temp/clarinet-tone-example.wav")WriteFile32
It really does not matter if that is meaningless to you! However, we can see some key points in there:(
?frequency,
(
((1,(?r,(?frequency,?frequency-spacing)*)ExactSinWave)DirectMix,?modulation-amount)NumericVolume
)Mix
)PhaseModulatedSinWave !signal
The above is the piece of the patch which actually does the modulation. It modulates the fundamental (given by the value ?frequency) by a sine wave at the modulation frequency which is given by ?frequency-spacing * ?frequency.
Also we have:
0.15 !modulation-amount 1.2 !frequency-spacing ((?play-bell-inner Do),"temp/bell-tone-example.wav")WriteFile32 0.35 !modulation-amount 1.002 !frequency-spacing ((?play-bell-inner Do),"temp/string-tone-example.wav")WriteFile32 0.5 !modulation-amount 2.0 !frequency-spacing ((?play-bell-inner Do),"temp/clarinet-tone-example.wav")WriteFile32
This is where the three tones are produced. Different spacing between fundamental and the modulation and different amounts of modulation are all that is required to produce completely different spectra and amazingly different sounding notes.
Frequency modulation is the moving of the fundamental frequency up and down. But that is quite hard to get right. The slightest numerical error and what we hear is the note being off pitch. To get frequency modulation correct, we need to exactly balance the up and down parts. This can prove quite hard to get right in practice. Fortunately, there is another property of a pure sine wave we can mess with which has the same effect for synthesis but is easier to work with.
Phase:
Again, this gets a little tricky to explain without a little mathematics. I will try really hard to make it as simple as possible! Let us look at the sine wave:
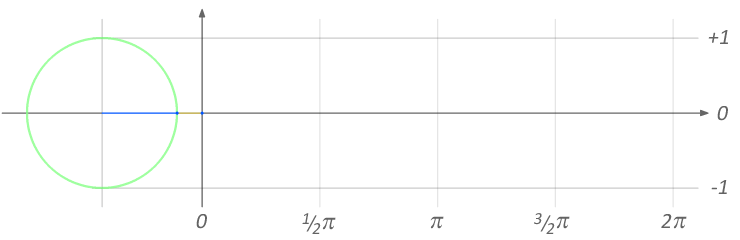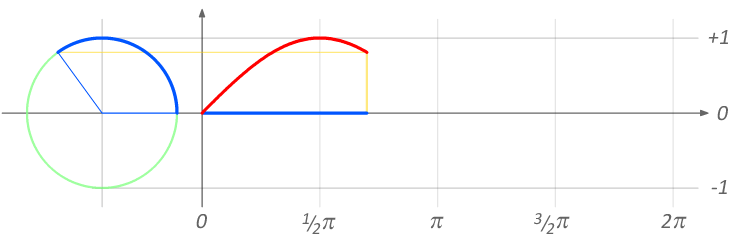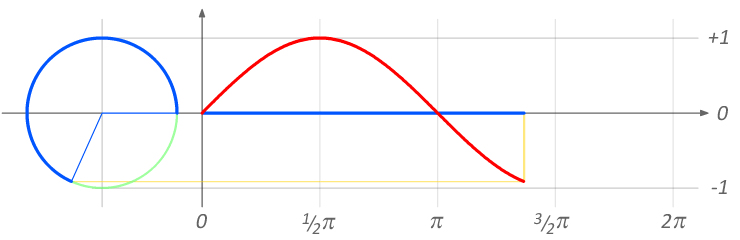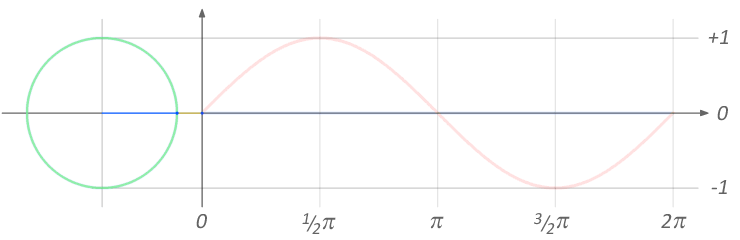 |
| This image is Wiki Commons - see here: http://en.wikipedia.org/wiki/File:Sine_curve_drawing_animation.gif |
If we imagine a spot of paint on a wheel at 3 o'clock and we roll that wheel along the ground, then just look at the hight of the spot we get a sine wave.
As the wheel rotates, we can see there is an angle between where the spot started,the centre of the wheel and where the spot is currently. For every value of this angle there is a value of the sin wave height.
This is effectively how the sine wave generator in a digital synthesiser works. It takes an angle which continually increases from 0 to 360 degrees (usually this is measured in radians but that is a detail) and for each tiny incremental step in the angle it looks up the value of a sine wave. Repeating this continuously produces a continuous sine wave which is what we call a 'Digital Oscillator'.
To phase modulate the digital oscillator we simply add a varying amount to the phase. This can change the instantaneous pitch but not the fundamental frequency. OK the mathematics here is a little more complex - feel free to stop reading this paragraph now.... Still here? OK, modulating the phase is the same as altering the first differential of the the wave form. But the first differential of a sine wave is a cosine wave which has the same shape. So, from the human perception point of view, except for instantaneous effects (transients - which I am not discussing here) phase and frequency modulation are exactly the same. The advantage is that if we get a slight asymmetry in the modulation it does not effect the fundamental as the rate of change asymmetry required to make the modulation asymmetrical cancels out the net effect.
To prove phase modulation does not effect the fundamental even when the modulator is asymmetrical I will modulate 440Hz with a rectified sine wave.
 |
| The same 440 modulated by 528 tone as above but with the 528Hz sine wave rectified to make an asymmetric wave form. |
We can clearly see that whilst the modulated signal now has many more, stronger inharmonics in it, the fundamental frequency has not changed.
Here is an example of piece of music created using phase modulation:
[Here is the patch for the above]
{
(
(0,0),
(?a,1),
(?d,0.5),
(?s,0.1)
(?r,0.0)
)NumericShape !env
(
(0,0),
((?a,2)/,1),
(?d,0),
(?r,0.0)
)NumericShape !hitEnv
(
(?d WhiteNoise,(?d,?pitch)ExactSinWave MakeSquare)Mix pcnt+50,
?hitEnv
)Multiply !hit
(>hit,(?pitch,2)*,2)ButterworthLowPass !hit
(
?pitch,
(
((1,(?r,(?pitch,?pitch-spacing)*)ExactSinWave)DirectMix,?ring-amount)NumericVolume
)Mix
)PhaseModulatedSinWave !signal
(
(
>signal,
>env
) Multiply Normalise,
?hit
)Mix Normalise
}!play-bell-inner
{
?play-bell-inner Do !s1
(>pitch,1.005)* !pitch
?play-bell-inner Do dbs-16 !s2
(>s1,>s2)Mix Normalise !signal
(
(?dullness,0)gt,
{
(>signal,?pitch,?dullness)BesselLowPass Normalise !signal
(>signal,?pitch,2)ButterworthHighPass Normalise !signal
},{}
)Choose Invoke
>signal
}!play-bell
{
(?velocity,1.5)** !volume
?play-bell Do !signal
(60000,?length)+ !length
{?length WhiteNoise}Do !reverb
{((>reverb,3.0)Power Normalise,10,1)ButterworthLowPass}Do !reverb
{((0,-99),(50,0),(?length,-60))SimpleShape}Do !renv
{(>reverb Normalise,>renv)Multiply}Do !reverb
{(>reverb,?r Silence)Concatenate}Do !reverb
{(>signal,?length Silence)Concatenate}Do !signal !signal-dry
?signal Magnitude !mag
{>signal FrequencyDomain}Do !signal
{>Reverb FrequencyDomain}Do !reverb
(?signal,?reverb)CrossMultiply !signal
>signal TimeDomain !signal
?signal Magnitude !newMag
(>signal,(>mag,>newMag)/)NumericVolume !signal-wet
(>signal-wet,>signal-dry)Mix Normalise !signal
((>signal,?pitch,1)ButterworthHighPass Normalise,(?volume,(0.25,Random)*)+)NumericVolume
}!reverb-bell
{
Bunch !notes
0 !count
0 !prev-high
(
?track,
{
^tickOn ^tickOff ^note ^key ^velocity
("Note ",?count)Println
(
(?count,?notesToPlay)lt,
{
[ Set up the note ]
(?tickOn,?beat)* !at
((?tickOff,?tickOn)-,?beat)* !length
(Semitone,?key)** !multi
(?baseSound,>multi)* !pitch
(>pitch,2)/ !pitch
(>velocity,100)/ !velocity
[ Play the note ]
((?voice Do,?at),>notes)AddEnd !notes
},{}
)Choose Invoke
(>count,1)+ !count
}
)InvokeAll
>notes MixAt Normalise
}!play
128 !pitch
1.2 !pitch-spacing
1 !dullness
0.15 !ring-amount
32 !a
128 !d
2048 !s
8192 !r
?reverb-bell !voice
"C0" Note !baseSound
48.00 !beat
"temp/chpn-p6.mid" ReadMidiFile
^t1
^t2
^t3
?t3 !track
999 !notesToPlay
?play Do !left
?play Do !right
((?left,?right),"temp/bell-preb.wav")WriteFile32

No comments:
Post a Comment