What is an Oscillator and how can we great one using a generator in Python?
An oscillator is something which naturally passes back and forth through some fixed or semi-fixed pattern. A simple but effective transistor based oscillator is a phase delay (or phase shift) circuit:
 |
| Wiki Commons - see here http://en.wikipedia.org/wiki/File:RC_phase_shift_oscillator.svg |
The output is delayed and fed back into the input. The output is the inverse of the input. This means that without the delay the circuit would do nothing at all. However, because there is a delay it oscillates making a sine wave. We can make a Python generator do very much the same thing:
from com.nerdscentral.audio import SFData
def oscillator(damping):
damping = float(damping)
weight = 0.1
value = 0.0
middle = value
yield 0,0
while(1):
if(value>middle):
weight-=damping
else:
weight+=damping
value+=weight
yield value,weight
It almost looks too simple to work but it does. The phase shift delay is not caused by 'recording' a sequence of output values and feeding them into the input (inverted). It is done by making the feedback cumulative. The variable weight is slowly shifted to oppose the variable value. If we plot the two variables as waves we get this:
 |
| Waveforms of weight and value. value top. weight bottom. These are not plotted to amplitude scale. The max value of wave is ca 50 and the max value of weight is ca .01 |
We can see from the above that weight is 90 degrees out of phase with value. We have made a phase delay oscillator. This approach makes a passible sine wave: However, the amplitude is not controlled at all that the produced wave for is not a very good sine wave.
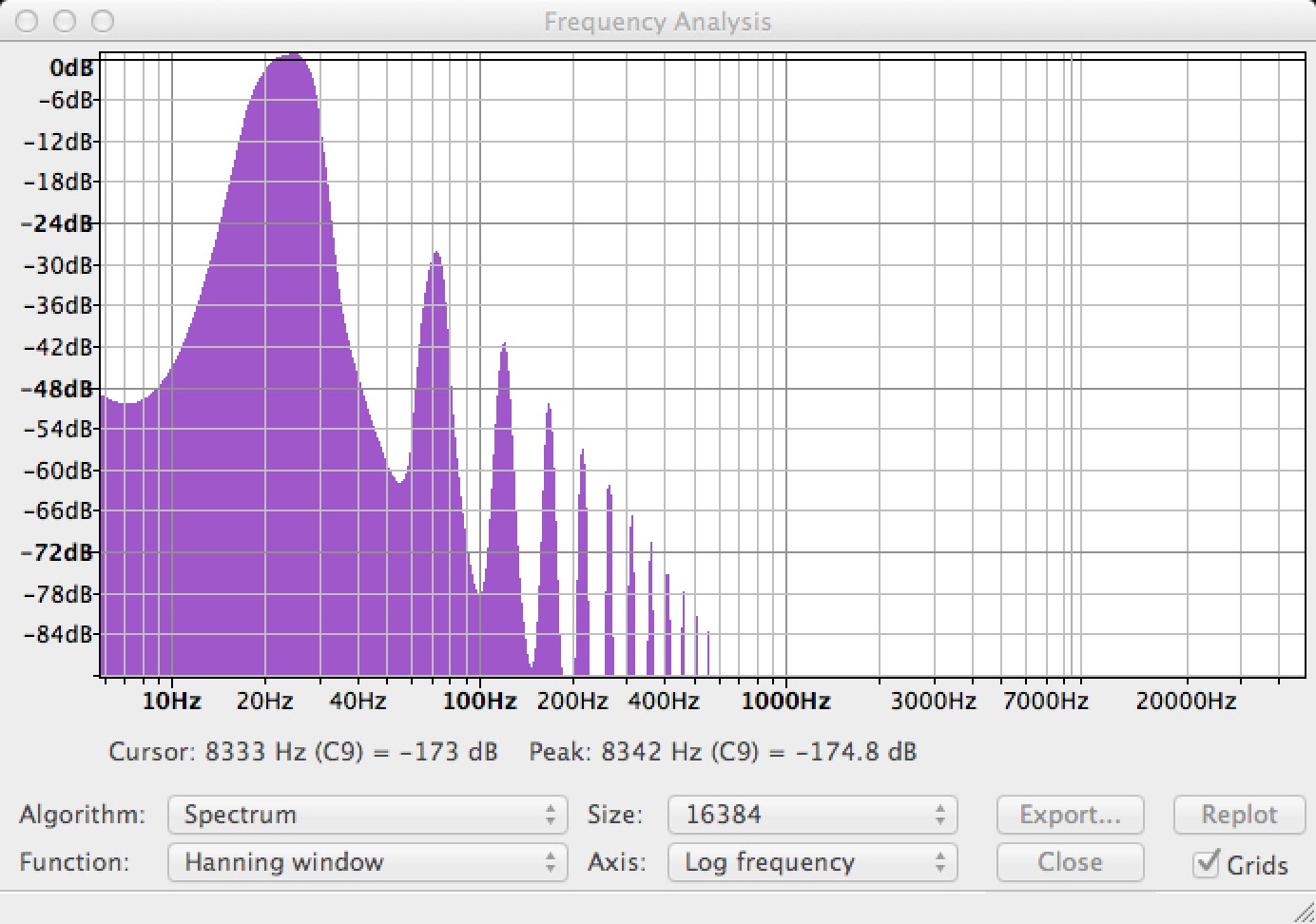 |
| The spectrum of our oscillator output. The large number and magnitude of harmonics shows it not to be a very pure sine wave. |
def oscillator(damping):
damping = float(damping)
lower = -1.0
upper = 1.0
weight = 0.1
value = 0.0
middle = value
yield 0,0
while(1):
if(value>middle):
weight-=damping
else:
weight+=damping
value+=weight
yield out,weight
if(out<lower):
value=prev
elif(out>upper):
value=prev
This addition locks the oscillator between +-1 and improves the sine wave quite a bit. The new spectrum looks like this (it is higher frequency for the given damping):
 |
| Slightly enhanced oscillator spectrum |
Let's Make Some Sounds
Making oscillators is fun, but now we have an analogue style oscillator in Python, we really have a moral responsibility to make sounds with it! Will the computational equivalent of analogue make more complex and interesting signals and traditional digital stuff? Here is a much more interesting version of the oscillator:
def oscilator(damping,asym=1.0,mixer=0):
damping = float(damping)
lower = -1.0
upper = 1.0
weight = 0.1
value = 0.0
middle = value
gain = 1.0
prev = 0.0
cross = 0.0
pos = 0.0
gainV = 0.9999
xcount = 0
asym = float(asym)
yield 0,0,0
while(1):
if(value>middle):
weight-=damping*asym
else:
weight+=damping
if(mixer != 0):
value+=mixer.next()
value+=weight
out=value*gain
yield out,weight,xcount
if(out<lower):
value=prev
gain*=gainV
elif(out>upper):
value=prev
gain*=gainV
elif(prev>0 and value<0):
gain/=gainV
xcount+=1
pos+=1
prev=value
def wobble(damping):
wosc=oscilator(damping,1.0)
while(1):
s,t,xs=wosc.next()
yield s*0.00001
The above uses recursive generators to make one oscillator inject instability into a second. We pass an instance of wobble into the mixer parameter of oscillator to get the effect. I have also added the ability to inject asymmetry into the oscillator to add harmonics. In have highlighted the bits of code which do these things.
We can put the output of our oscillator into a Sonic Field SFData object and then process it like any other sound:
from com.nerdscentral.audio import SFData
...
data=SFData.build(len)
for x in range(0,length):
s,t,xs=osc.next()
data.setSample(x,s)
Yes - it really is that simple to create an auto signal from a Python generator using Sython.
Warning - read the label carefully:
If you are familiar with the determinism of working with normal digital signals, this approach will come as a bit of a shock. What you end up with is unstable and pretty much unpredictable. Though the output signal is deterministic (you run it twice you get the same numbers) it is also highly unstable. That really nice sine wave I showed above is a 'attractor' for the equation. It is a well behaved oscillating attractor. What you get with the more complex recursive version is a 'strange attractor'; the signal does not repeat it self. It might not even be a real attractor but just a semi-stable state from which, after enough cycles, the system will escape. Also, forget normal tuning, the output frequency is not linearly dependant on the input one. To get any sort of accurate pitch I would suggest counting the crossovers and then changing the sample rate to lock the pitch to that required.
First Creation:
Above is the first creation I have made with this new technique. It is not music at all. I wanted to create a sound into which the listener is placed which conveys the menace of WWII era piston engine aircraft. The very rich and ever changing 'analogue' nature of the oscillators does this in a way much more convincing that I think I could have managed using the normal sine wave generator and post processing approach of digital synthesis (or at least, not as easily).
Here is the patch which created the piece:
import math
import random
from com.nerdscentral.audio import SFData
def fixSize(signal):
mag=sf.MaxValue(signal)
return sf.NumericVolume(signal,1.0/mag)
def nullMixer():
while(1):
yield 0
def oscilator(damping,asym=1.0,mixer=0):
damping = float(damping)
lower = -1.0
upper = 1.0
weight = 0.1
value = 0.0
middle = value
gain = 1.0
prev = 0.0
cross = 0.0
pos = 0.0
gainV = 0.9999
xcount = 0
asym = float(asym)
yield 0,0,0
while(1):
if(value>middle):
weight-=damping*asym
else:
weight+=damping
if(mixer != 0):
value+=mixer.next()
value+=weight
out=value*gain
yield out,weight,xcount
if(out<lower):
value=prev
gain*=gainV
elif(out>upper):
value=prev
gain*=gainV
elif(prev>0 and value<0):
gain/=gainV
xcount+=1
pos+=1
prev=value
def wobble(damping):
wosc=oscilator(damping,1.0)
while(1):
s,t,xs=wosc.next()
#print s
yield s*0.00001
def invasion(d1,d2,seconds):
osc1=oscilator(d1,2,wobble(0.000020))
osc2=oscilator(d1,2,wobble(0.000015))
osc3=oscilator(d1,2,wobble(0.000010))
osc4=oscilator(d1,2,wobble(0.000005))
osc5=oscilator(d2,1.5,wobble(0.000020))
osc6=oscilator(d2,1.5,wobble(0.000015))
osc7=oscilator(d2,1.5,wobble(0.000010))
osc8=oscilator(d2,1.5,wobble(0.000005))
length=96000*seconds
xs=0
def drone(osc,len):
def doDrone():
data=SFData.build(len)
print "Doing Drone"
for x in range(0,length):
s,t,xs=osc.next()
data.setSample(x,s)
# Go to a lot of effort to remove
# clicks due to DC offset of the start and end
l=sf.Length(data)
data=sf.ButterworthHighPass(sf.Normalise(data),10,2)
data=sf.Multiply(
data,
sf.NumericShape((0,0),(256,0),(l/2,1),(l-256,0),(l,0))
)
data=sf.Multiply(
sf.Saturate(data),
sf.NumericShape((0,0),(256,1),(l-256,1),(l,0))
)
return sf.Realise(data)
return sf_do(doDrone)
data1=drone(osc1,length)
data2=drone(osc2,length)
data3=drone(osc3,length)
data4=drone(osc4,length)
data5=drone(osc5,length)
data6=drone(osc6,length)
data7=drone(osc7,length)
data8=drone(osc8,length)
def mix1():
return sf.Realise(
fixSize(
sf.MixAt(
(sf.Pcnt10(data2),30),
(sf.Pcnt20(data3),20),
(data1,0),
(data4,0),
(sf.Pcnt10(data6),30),
(sf.Pcnt20(data7),20),
(data5,0),
(data8,0)
)
)
)
def mix2():
return sf.Realise(
fixSize(
sf.MixAt(
(sf.Pcnt10(data1),30),
(sf.Pcnt20(data4),20),
(data2,0),
(data3,0),
(sf.Pcnt10(data6),30),
(sf.Pcnt20(data7),20),
(data5,0),
(data8,0)
)
)
)
dataL=sf_do(mix1)
dataR=sf_do(mix2)
return (dataL,dataR)
dataL1,dataR1=invasion(0.000025,0.000015,45)
dataL2,dataR2=invasion(0.000020,0.000007,45)
dataL3,dataR3=invasion(0.000011,0.000010,45)
dataL4,dataR4=invasion(0.000010,0.000012,45)
dataL=sf.Normalise(
sf.MixAt(
(dataL1, 0),
(dataL2, 30000),
(dataL3, 60000),
(dataL1, 90000),
(dataL4,120000),
(dataL1,150000),
(dataL4,160000)
)
)
dataR=sf.Normalise(
sf.MixAt(
(dataR1, 0),
(dataR2, 30000),
(dataR3, 60000),
(dataR1, 90000),
(dataR4,120000),
(dataR1,150000),
(dataR4,160000)
)
)
sf.WriteFile32((dataL,dataR),"temp/temp.wav")
dataL=0
dataR=0
def reverbInner(signal,convol,grainLength):
def reverbInnerDo():
mag=sf.Magnitude(signal)
if mag>0:
signal_=sf.Concatenate(signal,sf.Silence(grainLength))
signal_=sf.FrequencyDomain(signal_)
signal_=sf.CrossMultiply(convol,signal_)
signal_=sf.TimeDomain(signal_)
newMag=sf.Magnitude(signal_)
signal_=sf.NumericVolume(signal_,mag/newMag)
# tail out clicks due to amplitude at end of signal
l=sf.Length(signal_)
sf.Multiply(
sf.NumericShape(
(0,1),
(l-100,1),
(1,0)
),
signal_
)
return signal_
else:
return signal
return sf_do(reverbInnerDo)
def reverberate(signal,convol):
def reverberateDo():
grainLength = sf.Length(convol)
convol_=sf.FrequencyDomain(sf.Concatenate(convol,sf.Silence(grainLength)))
signal_=sf.Concatenate(signal,sf.Silence(grainLength))
out=[]
for grain in sf.Granulate(signal_,grainLength):
(signal_,at)=grain
out.append((reverbInner(signal_,convol_,grainLength),at))
return sf.Normalise(sf.MixAt(out))
return sf_do(reverberateDo)
(left,right)=sf.ReadFile("temp/temp.wav")
(convoll,convolr)=sf.ReadFile("temp/revb.wav")
wleft =reverberate(left,convoll)
wright=reverberate(right,convolr)
left=sf.Normalise(sf.MixAt(
(sf.Pcnt40(wleft),10),
(sf.Pcnt5(wright),40),
(sf.Pcnt5(wleft),120),
(sf.Pcnt45(left),0),
(sf.Pcnt5(right),110)
))
right=sf.Normalise(sf.MixAt(
(sf.Pcnt40(wright),10),
(sf.Pcnt5(wleft),40),
(sf.Pcnt5(wright),130),
(sf.Pcnt45(right),0),
(sf.Pcnt5(left),105)
))
sf.WriteFile32((left,right),"temp/temp_post.wav")

No comments:
Post a Comment